深度解析 K-Means 聚类算法：优缺点与应用 – wiki基地

作者： /

深度解析 K-Means 聚类算法：优缺点与应用

在数据挖掘和机器学习领域，聚类算法扮演着至关重要的角色。它们能够将海量数据中相似的数据点归集到一起，形成不同的“簇”，从而揭示数据内在的结构和模式。K-Means 算法作为一种经典且广泛应用的聚类算法，以其简单、高效的特性，在诸多领域都发挥着重要作用。本文将深入剖析 K-Means 算法的原理、实现步骤、优缺点，并结合实际应用场景，全面解析这一经典算法。

一、 K-Means 算法原理

1.1 核心思想

K-Means 算法的核心思想可以用一句话概括：将 n 个数据点划分到 k 个簇中，使得每个数据点都属于离其最近的簇中心（质心）所在的簇，同时使得簇内的平方误差和（SSE）最小化。

这里的关键要素有三个：

  • 簇（Cluster）： 相似数据点的集合。
  • 簇中心（Centroid）： 也称为质心，是簇内所有数据点各个维度的均值。
  • 平方误差和（SSE）： 每个数据点到其所属簇中心的距离的平方和，用于衡量聚类效果的好坏。SSE 越小，表示簇内数据点越紧密，聚类效果越好。

1.2 算法流程

K-Means 算法的流程可以概括为以下几个步骤：

  1. 初始化：

    • 随机选择 k 个数据点作为初始簇中心（质心）。
    • 或者使用其他方法（如 K-Means++）来选择初始簇中心。

  2. 分配：

    • 对于每个数据点，计算其与每个簇中心的距离（通常使用欧氏距离）。
    • 将该数据点分配给距离其最近的簇中心所在的簇。

  3. 更新：

    • 对于每个簇，重新计算其簇中心（即簇内所有数据点各个维度的均值）。

  4. 迭代：

    • 重复步骤 2 和 3，直到满足以下条件之一：
      • 簇中心不再发生变化（或变化很小）。
      • 达到预先设定的最大迭代次数。

1.3 算法图解

为了更直观地理解 K-Means 算法，我们可以通过一个简单的二维数据集的例子来演示其聚类过程：

  1. 初始化： 假设我们要将数据点分为 2 个簇（k=2），随机选择两个数据点作为初始簇中心（红色和蓝色）。
  2. 分配： 计算每个数据点到两个簇中心的距离，并将它们分配到最近的簇。
  3. 更新： 重新计算每个簇的簇中心（红色和蓝色十字）。
  4. 迭代： 重复分配和更新步骤，直到簇中心不再发生变化。

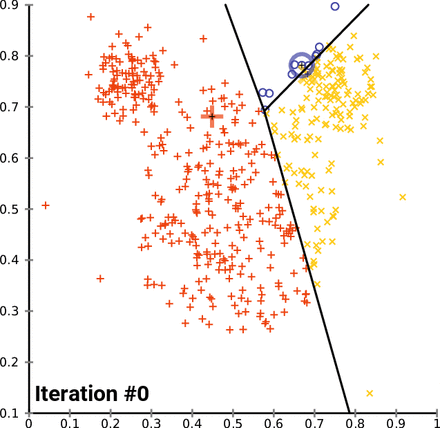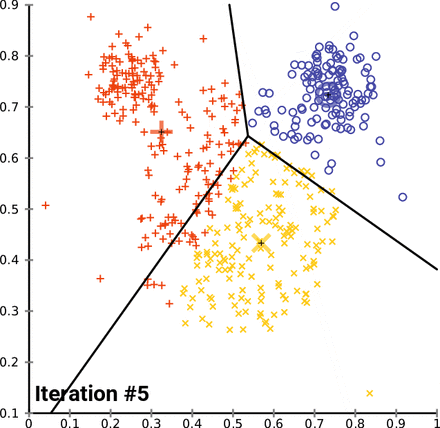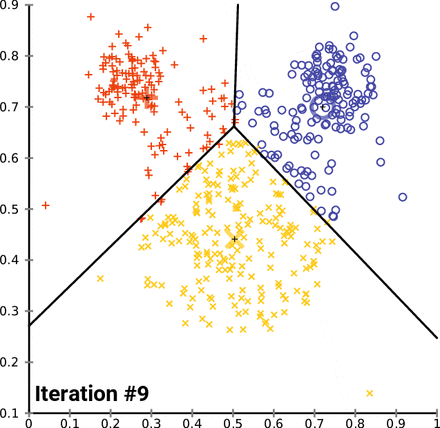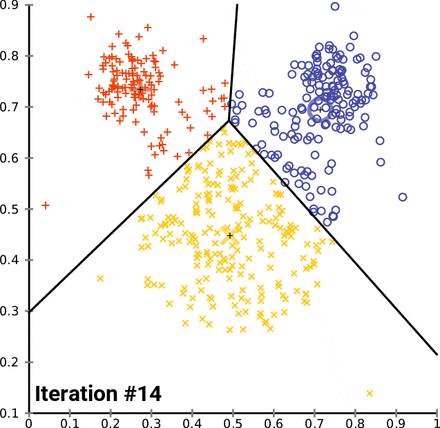
K-Means 算法图解

（图片来源：Wikimedia Commons）

二、 K-Means 算法实现

2.1 Python 实现

我们可以使用 Python 的 Scikit-learn 库来快速实现 K-Means 算法：

“`python
from sklearn.cluster import KMeans
import numpy as np

创建一个示例数据集

X = np.array([[1, 2], [1.5, 1.8], [5, 8], [8, 8], [1, 0.6], [9, 11]])

创建 KMeans 对象，设置簇的数量为 2

kmeans = KMeans(n_clusters=2)

训练模型

kmeans.fit(X)

获取簇中心

centroids = kmeans.cluster_centers_
print(“簇中心：”, centroids)

获取每个数据点所属的簇

labels = kmeans.labels_
print(“数据点所属的簇：”, labels)

预测新数据点所属的簇

new_data = np.array([[2, 2], [8, 9]])
predictions = kmeans.predict(new_data)
print(“新数据点所属的簇：”, predictions)
“`

2.2 关键参数

在 Scikit-learn 的 KMeans 类中，有一些重要的参数可以调整：

  • n_clusters：簇的数量（k 值），这是 K-Means 算法中最重要的参数。
  • init：初始簇中心的选择方法，默认为 k-means++，也可以设置为 random（随机选择）或传入一个数组来指定初始簇中心。
  • n_init：使用不同的初始簇中心运行 K-Means 算法的次数，默认为 10。算法会返回最佳的聚类结果（SSE 最小）。
  • max_iter：最大迭代次数，默认为 300。
  • tol：簇中心变化的容差，默认为 1e-4。当簇中心的变化小于该值时，算法停止迭代。

三、 K-Means 算法的优缺点

3.1 优点

  • 简单高效： K-Means 算法的原理简单，实现容易，计算效率高，时间复杂度接近线性，适合处理大规模数据集。
  • 可解释性强： 聚类结果直观，每个簇都由其簇中心来表示，易于理解和解释。
  • 可扩展性好： 对于新的数据点，可以很容易地将其分配到已有的簇中。

3.2 缺点

  • 需要预先指定 k 值： k 值的选择对聚类结果影响很大，但在实际应用中，k 值往往难以预先确定。
  • 对初始簇中心敏感： 不同的初始簇中心可能导致不同的聚类结果，算法可能收敛到局部最优解，而不是全局最优解。
  • 对异常值敏感： 异常值（离群点）可能会对簇中心的计算产生较大影响，导致聚类结果偏差。
  • 不适用于非凸形状的簇： K-Means 算法假设簇是凸形的（球形），对于非凸形状的簇，聚类效果较差。
  • 对数据分布有假设： K-Means 算法假设数据是各向同性的，即各个维度上的方差相同。如果数据分布不满足这一假设，聚类效果也会受到影响。

四、 K-Means 算法的改进

针对 K-Means 算法的缺点，研究者们提出了许多改进方法：

4.1 K-Means++

K-Means++ 是一种改进的初始簇中心选择方法，它可以有效地避免 K-Means 算法收敛到局部最优解。其基本思想是：

  1. 从数据集中随机选择一个数据点作为第一个簇中心。
  2. 对于每个数据点，计算其与已选择的簇中心的距离（D(x)）。
  3. 选择下一个簇中心，使得被选择的概率与 D(x) 的平方成正比。
  4. 重复步骤 2 和 3，直到选择了 k 个簇中心。

K-Means++ 的核心思想是让初始簇中心尽可能分散开来，从而提高聚类结果的质量。

4.2 Mini-Batch K-Means

Mini-Batch K-Means 是一种适用于大规模数据集的 K-Means 变体。它每次只使用数据集的一部分（mini-batch）来更新簇中心，而不是使用全部数据，从而大大减少了计算时间。

Mini-Batch K-Means 的算法流程与 K-Means 类似，只是在更新簇中心时，只使用随机选择的一部分数据点。这会带来一定的随机性，但通常可以在计算效率和聚类效果之间取得较好的平衡。

4.3 二分 K-Means

二分 K-Means 是一种层次聚类方法，它可以克服 K-Means 对初始簇中心敏感的问题。其基本思想是：

  1. 将所有数据点作为一个簇。
  2. 将该簇一分为二，选择 SSE 最大的簇进行分裂。
  3. 重复步骤 2，直到达到预先设定的簇的数量。

二分 K-Means 每次分裂都选择 SSE 最大的簇，这有助于避免局部最优解。

4.4 K-Medoids

K-Medoids 算法与 K-Means 类似，但它选择簇中实际的数据点作为簇中心（称为 medoid），而不是使用均值。这使得 K-Medoids 算法对异常值不敏感。

K-Medoids 算法的流程与 K-Means 类似，只是在更新簇中心时，选择簇内与其他数据点距离之和最小的数据点作为新的 medoid。

4.5 Canopy 聚类

Canopy 聚类是一种粗聚类算法，通常与 K-Means 结合使用。它可以快速地将数据点划分到一些重叠的“canopy”中，每个 canopy 中的数据点被认为是相似的。然后，可以使用 K-Means 算法对每个 canopy 中的数据点进行更精细的聚类。

Canopy 聚类可以有效地减少 K-Means 算法的计算量，特别是对于高维数据集。

五、 K-Means 算法的应用

K-Means 算法在各个领域都有广泛的应用，以下列举一些典型的应用场景：

5.1 客户细分

在市场营销中，K-Means 算法可以根据客户的购买行为、人口统计特征、兴趣爱好等信息，将客户划分为不同的群体，从而实现精准营销。例如，可以将客户分为“高价值客户”、“潜在客户”、“流失客户”等，针对不同的客户群体制定不同的营销策略。

5.2 图像分割

在图像处理中，K-Means 算法可以根据像素的颜色、纹理等特征，将图像分割成不同的区域。例如，可以将图像中的前景和背景分离，或者将图像中的不同物体分割出来。

5.3 文档聚类

在文本挖掘中，K-Means 算法可以根据文档的词频、主题等特征，将文档划分为不同的类别。例如，可以将新闻文章按照主题分类，或者将用户评论按照情感分类。

5.4 异常检测

K-Means 算法可以用于检测数据集中的异常值（离群点）。通过将数据点聚类，可以将远离簇中心的数据点视为异常值。例如，可以用于检测信用卡欺诈、网络入侵等。

5.5 推荐系统

K-Means 算法可以用于构建推荐系统。通过将用户或物品聚类，可以找到与用户兴趣相似的其他用户，或者与用户喜欢的物品相似的其他物品，从而进行推荐。

5.6 基因表达数据分析

在生物信息学中，K-Means 算法可以用于分析基因表达数据。通过将基因表达谱相似的基因聚类，可以发现具有相似功能的基因，或者识别与特定疾病相关的基因。

六、 总结

K-Means 算法作为一种简单高效的聚类算法，在数据挖掘和机器学习领域有着广泛的应用。它易于理解和实现，能够处理大规模数据集。然而，K-Means 算法也存在一些缺点，如需要预先指定 k 值、对初始簇中心敏感、对异常值敏感等。针对这些缺点，研究者们提出了许多改进方法，如 K-Means++、Mini-Batch K-Means、二分 K-Means、K-Medoids 等。

在实际应用中，我们需要根据具体的数据集和应用场景，选择合适的 K-Means 算法变体，并进行参数调优，以获得最佳的聚类效果。同时，我们也需要结合其他数据分析方法，对聚类结果进行深入解读和验证，从而更好地理解数据，发现有价值的信息。

发表评论

您的邮箱地址不会被公开。 必填项已用 * 标注

滚动至顶部